ライフプランニングの考え方・手法(全12問中2問目)
No.2
Aさん(50歳)は、毎年一定金額を積み立て、65歳の時点で、現在の価値で2,000万円を貯めたいと考えている。今後15年間について毎年2%ずつ物価が上昇していくと仮定した場合、50歳から65歳までの15年間の毎年の積立額として、次のうち最も適切なものはどれか。なお、現在の貯蓄額は0円とし、積立期間の運用利回り(複利)は年5%、積立は年1回行うものとする。また、下記の係数表を利用して算出し、計算結果における万円未満を切り捨て、手数料や税金等は考慮しないものとする。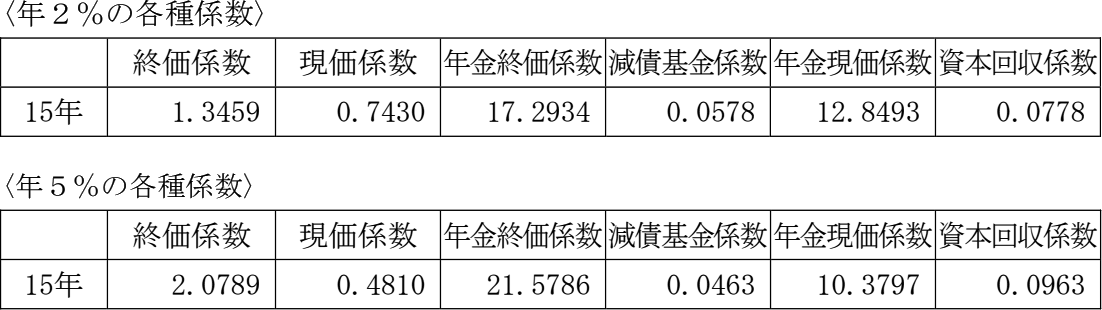
2024年5月試験 問1
- 92万円
- 124万円
- 179万円
- 259万円
広告
正解 2
問題難易度
肢114.3%
肢272.0%
肢39.2%
肢44.5%
肢272.0%
肢39.2%
肢44.5%
分野
科目:A.ライフプランニングと資金計画細目:3.ライフプランニングの考え方・手法
解説
65歳時点で必要となる額を求めた後、その額を積み立てるのに必要な毎年の積立額を求めるという2段階の計算が必要となります。物価が上昇していく場合、同じ金額で買えるモノの量は徐々に減っていくので、お金の価値は目減りしていきます。毎年2%ずつ物価が上昇していく状況において、15年後に現在の価値で2,000万円に相当する金額は、終価係数を用いて求めることができます※。
2,000万円×1.3459=2,691.8万円
※現価係数を使って、2,000万円=●×0.7430 で求めることもできます。
65歳時点で貯めたい金額は2,691.8万円とわかります。一定の利率で複利運用しながら、一定期間経過後に目標額を得るために必要となる毎年の積立額は、減債基金係数を用いて求めます。
2,691.8万円×0.0463=124.6…万円
(万円未満切り捨て)124万円
したがって[2]が正解となります。
広告