• Home
• 2024年1月試験
• 学科 問1

FP1級過去問題 2024年1月学科試験 問1(改題)

問1

Aさん（55歳）は、妻Bさん（50歳）との2人暮らしである。Aさんは65歳から20年にわたって、夫婦2人の公的年金と老後資金の取崩しの合計で毎年300万円を受け取りたいと考えている。Aさんの65歳から支給される公的年金の年金額が毎年180万円、妻Bさんの65歳から支給される公的年金の年金額が毎年75万円である場合、毎年300万円を受け取るためにAさんが65歳時点で準備する必要がある老後資金の金額として、次のうち最も適切なものはどれか。
なお、取崩期間中の運用利率は年3％、取崩しは年1回行うものとする。また、下記の係数表を利用して算出し、計算過程および計算結果は万円未満を切り捨て、税金や手数料等は考慮しないものとする。

解説

Aさんが65歳から受け取れる公的年金は年額180万円なので、300万円のうち120万円を老後資金の取崩しで賄うことになります。その後、Aさんが70歳になると、妻Bさんも65歳になって年額75万円の公的年金を受け取れるようになるので、それ以降15年間は、300万円のうち2人の年金額「180万円＋75万円＝255万円」で足りない45万円を老後資金の取崩しで賄うことになります。これを整理したのが下図です。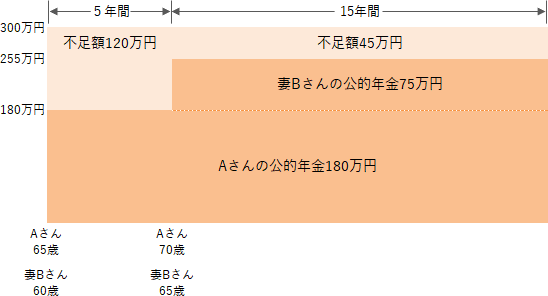

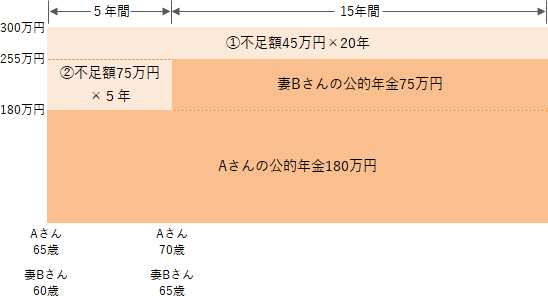
本問では15年の係数が用意されていないので、Aさんが70歳時点で必要となる資金を求めることができません。しかし、少し視点を変えて、①45万円を20年間受け取る、②「120万円－45万円＝75万円」を5年間受け取るというように分割することで、5年と20年の係数を使って原資を求めることができます。

原資を複利運用しながら毎年一定額を取り崩す場合に、必要となる原資を求めるには「年金現価係数」を使います。①は20年の年金現価係数、②には5年の年金現価係数を用いてそれぞれ必要となる原資を求め、それを合計します。

　45万円×14.8775＋75万円×4.5795
＝669.4875万円＋343.4775万円
＝1,012.965万円
（万円未満切り捨て）1,012万円

したがって[3]が正解です。

• 次の問題(問2)