• Home
• 2018年1月試験
• 学科 問6

FP1級過去問題 2018年1月学科試験 問6

問6

3,000万円を年3％で複利運用しながら20年間、毎年120万円ずつ取り崩した場合、20年後に残っている金額として、次のうち最も適切なものはどれか。なお、取崩しは年1回であるものとし、下記の係数を使用して算出すること。また、税金や手数料等は考慮せず、計算結果は万円未満を四捨五入すること。

解説

まず、20年間にわたり毎年120万円を受け取るのに必要な年金原資を計算し、3,000万円からその金額を控除することで残額を求めます。

「毎年均等に取り崩して受け取る」とくれば、使用できるのは「資本回収係数」または「年金現価係数」のいずれかです。設問のケースでは毎年の取り崩す金額が決まっており、そのために必要な元本を知りたいため「年金現価係数」を用います。

しかし、本問では年金現価係数が与えられていないため、対になる資本回収係数を用いる必要があります。

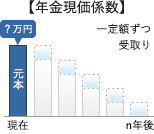
年金原資と毎年の受取額及び資本回収係数には以下の関係があります。

　年金原資×資本回収係数＝毎年の年金額

つまり、毎年の年金額から年金原資を求める方法には年金現価係数を乗じること以外にも、以下のように毎年の年金額を資本回収係数で除す方法が使えることになります。

　年金原資＝毎年の年金額÷資本回収係数

本問ではこの式を使って年金原資を求めます。年利3％、期間20年の資本回収係数は0.0672なので、

　120万円÷0.0672＝1,785.714…万円
（万円未満を四捨五入）1,786万円

3,000万円から年金原資を控除した金額は、

　3,000万円－1,786万円＝1,214万円

さらに、この1,215万円についても20年間複利運用するので増えることを考えなくてはなりません。元本がわかっていて、それを一定期間にわたり複利運用したときの元利合計額を求めるには「終価係数」を用います。

　1,214万円×1.8061＝2,192.6054万円
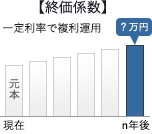
（万円未満を四捨五入）2,193万円

したがって[3]が正解です。

• 前の問題(問5)
• 次の問題(問7)