FP1級 2022年5月　応用編 問56

【この問題にはが用意されています。読んでから回答してください。】
　Aさん（46歳）は、企業の安全性を重視して、長期的なスタンスで投資したいと思っている。具体的には、製造業の上場企業X社に興味があり、下記の財務データを参考にして、投資判断を行いたいと考えている。また、投資信託についてはYファンドとZファンドの購入を考えている。Aさんは、X社株式や投資信託の購入にあたり、NISAを利用してみたいと考えている。
　そこで、Aさんは、ファイナンシャル・プランナーのMさんに相談することにした。

〈2024年3月期のX社の財務データ等〉（単位：百万円）
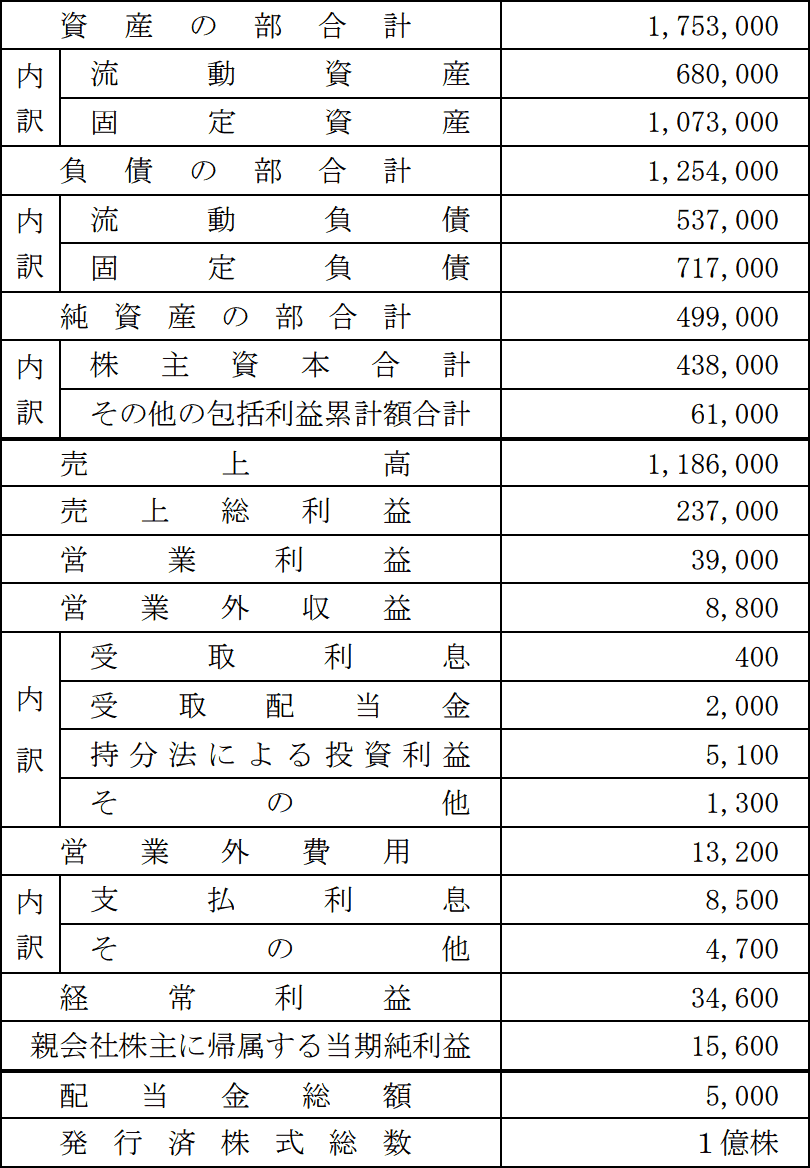
b1.png./image-size:405×584
  • 中間配当の権利確定日：2024年9月30日（金）
〈Yファンド・Zファンドの実績収益率・標準偏差・共分散〉
b2.png./image-size:516×86
  • 上記以外の条件は考慮せず、各問に従うこと。

問56

《設例》の〈Yファンド・Zファンドの実績収益率・標準偏差・共分散〉に基づいて、①YファンドとZファンドの相関係数、②Yファンドのシャープ・レシオ、③YファンドとZファンドをそれぞれ6：4の割合で購入した場合のポートフォリオの標準偏差を、それぞれ求めなさい。〔計算過程〕を示し、〈答〉は表示単位の小数点以下第3位を四捨五入し、小数点以下第2位までを解答すること。なお、シャープ・レシオについては、安全資産利子率を0.10％として計算すること。
① 
② 
③％

正解　

① 0.32
80.0010.00×25.00＝0.32
② 0.59
6.00％－0.10％10.00％＝0.59
③ 13.21（％）
0.62×10.02＋0.42×25.02＋2×0.6×0.4×0.32×10.0×25.0＝174.4
174.4＝13.21％（小数点以下第3位四捨五入）

分野

科目：C.金融資産運用
細目：9.ポートフォリオ運用

解説

〔①について〕
2資産の相関係数、標準偏差および共分散には次式の関係があります。

　相関係数＝共分散A資産の標準偏差×B資産の標準偏差
　※分母は％のまま計算します

本問では標準偏差と共分散がわかっているので、2つを使って相関係数を求めます。Yファンドの標準偏差は10％、Zファンドの標準偏差は25％、共分散は80なので、

　8010%×25%＝80250＝0.32

よって、正解は0.32となります。

※相関係数は－1～＋1までの値をとることに注意して計算しましょう。

〔②について〕
シャープ・レシオは、ポートフォリオの超過収益率を標準偏差で除して求めます。

　シャープ・レシオ＝ポートフォリオの収益率－安全資産利子率標準偏差

Yファンドの収益率は6％、標準偏差は10％、安全資産利子率は0.1％ですから、

　6－0.110＝0.59

よって、正解は0.59となります。

〔③について〕
A・Bという2つの資産から成るポートフォリオの標準偏差は、以下の式で求めます。

　A＝標準偏差A×組入比率A
　B＝標準偏差B×組入比率B
　分散＝A2＋B2＋(2×A×B×相関係数)
　標準偏差＝分散

上記の式にYファンドとZファンドの値を当てはめます。相関係数は①で求めた0.32を使います。

　A＝10×0.6＝6
　B＝25×0.4＝10
　分散＝62＋102＋(2×6×10×0.32)＝36＋100＋120×0.32＝174.4
　174.4＝13.206…％
（小数点以下第3位四捨五入）13.21％

よって、正解は13.21(％)となります。
広告