FP1級過去問題 2025年5月学科試験 問1
問1
会社員のAさん(60歳)は、手元資金15,000千円のうち、8,000千円を15年間にわたって毎年均等に取り崩し、残りの7,000千円についてはそのまま5年間運用し、その後、10年間にわたって毎年均等に取り崩すことを考えている。この場合、65歳から75歳までの10年間の毎年の取崩額として、次のうち最も適切なものはどれか。 なお、取崩期間および5年間の運用期間中の運用利回り(複利)は年3%とし、取崩しは年1回行うものとする。また、下記の係数表を利用して算出し、計算結果は千円未満を切り捨て、手数料や税金等は考慮しないものとする。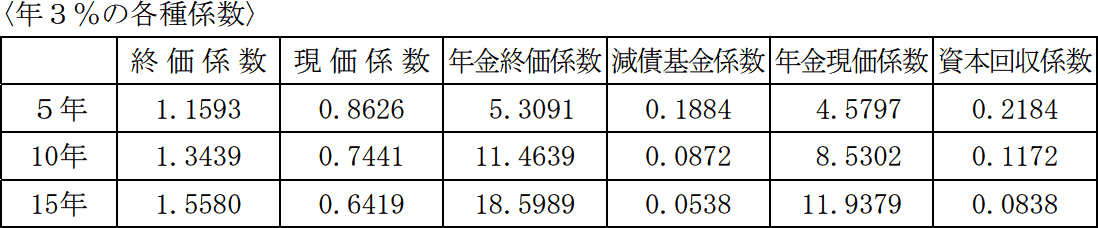

- 1,138千円
- 1,217千円
- 1,495千円
- 1,621千円
広告
広告
正解 4
問題難易度
肢116.0%
肢214.1%
肢316.6%
肢453.3%
肢214.1%
肢316.6%
肢453.3%
分野
科目:A.ライフプランニングと資金計画細目:3.ライフプランニングの考え方・手法
解説
65歳から75歳までの期間における資産の取崩し額は、次の2つの合計額です。- 8,000千円を15年間にわたり取り崩した額
- 7,000千円を5年間複利運用した額を、10年間にわたり取り崩した額

8,000千円×0.0838=670.4千円 … ①
次にb.を求めます。「終価係数」で5年間の複利運用後の金額を求め、「資本回収係数」で10年間の各年の取崩し額を計算します。
7,000千円×1.1593=8,115.1千円
8,115.1千円×0.1172=951.08…千円 … ②
65歳から75歳までの取崩額は①と②の合計です。
670.4千円+951.08…千円=1,621.48…千円
(千円未満切り捨て)1,621千円
したがって[4]が正解です。
広告
広告