FP1級 2025年5月　応用編 問56

【この問題にはが用意されています。読んでから回答してください。】
　Aさん（30歳）は、上場株式と公募株式投資信託への投資を行いたいと考えている。Aさんは、上場株式についてはX社株式（東京証券取引所上場銘柄）に興味を持ち、公募株式投資信託については投資信託Yと投資信託Zの購入を考えている。
　そこで、Aさんは、ファイナンシャル・プランナーのMさんに相談することにした。

〈X社の財務データ〉（単位：百万円）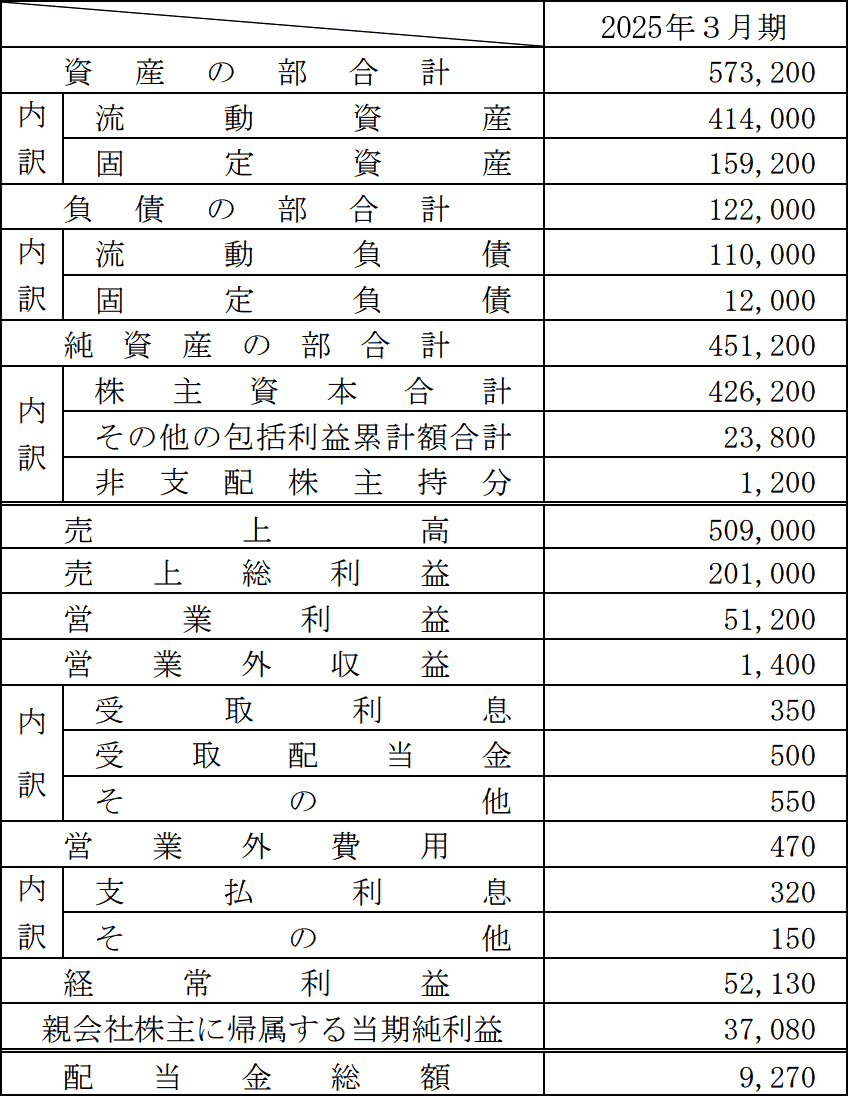
b1.png/image-size:424×548
〈投資信託Y・投資信託Zの予想収益率〉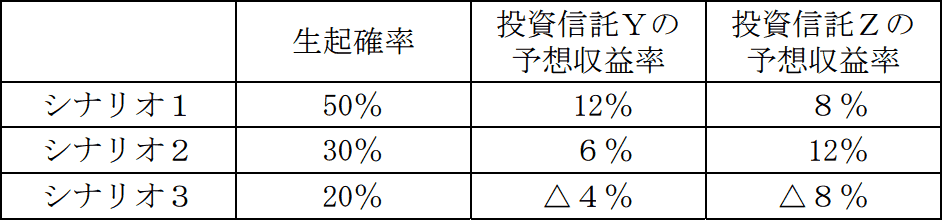
b2.png/image-size:471×110
  • 上記以外の条件は考慮せず、各問に従うこと。
広告

問56

《設例》の〈投資信託Y・投資信託Zの予想収益率〉に基づいて、次の①および②に答えなさい。〔計算過程〕を示し、〈答〉は表示単位の小数点以下第3位を四捨五入し、小数点以下第2位までを解答すること。

  1. 投資信託Yと投資信託Zを6：4の割合で組み入れたポートフォリオの期待収益率はいくらか。
  2. 投資信託Yと投資信託Zを6：4の割合で組み入れたポートフォリオの標準偏差はいくらか。
①％
②％
広告

正解　

① 6.60（％）
12％×0.5＋6％×0.3＋(－4％)×0.2＝7％
8％×0.5＋12％×0.3＋(－8％)×0.2＝6％
7％×0.6＋6％×0.4＝6.60％
② 6.16（％）
12％×0.6＋8％×0.4＝10.4％
6％×0.6＋12％×0.4＝8.4％
(－4％)×0.6＋(－8％)×0.4＝－5.6％
(10.4%－6.6%)×0.5+(8.4%－6.6%)×0.3+(－5.6%－6.6%)×0.2
＝6.16％（小数点以下第3位四捨五入）

分野

科目：C.金融資産運用
細目：9.ポートフォリオ運用

解説

〔①について〕
2資産から成るポートフォリオにおける、生起確率を踏まえた予想収益率は、各投資信託の予想収益率の期待値を投資信託の組入比率で加重平均した値となります。
投資信託Yの予想収益率の期待値
12％×0.5＋6％×0.3＋△4％×0.2＝7％
投資信託Zの予想収益率の期待値
8％×0.5＋12％×0.3＋△8％×0.2＝6％
組入比率は、投資信託Y：投資信託Z＝6：4なので、

　7％×0.6＋6％×0.4＝6.6％
（小数点以下第2位まで解答）6.60％

よって、正解は6.60(％)になります。

【別解】
シナリオごとの期待収益率を、シナリオごとの生起確率で加重平均する方法でも計算可能です。こちらで計算すると②標準偏差の計算が楽になります。
シナリオ1の予想収益率
12%×0.6＋8％×0.4＝7.2＋3.2＝10.4%
シナリオ2の予想収益率
6%×0.6＋12%×0.4＝3.6＋4.8＝8.4%
シナリオ3の予想収益率
△4%×0.6＋△8%×0.4＝△2.4＋△3.2＝△5.6%
生起確率は、シナリオ1：シナリオ2：シナリオ3＝50：30：20なので、

　10.4%×0.5＋8.4%×0.3＋△5.6%×0.2＝5.2＋2.52＋△1.12＝6.60%

〔②について〕
生起確率を踏まえたポートフォリオの標準偏差は、以下の手順で求めます。

　標準偏差＝∑生起確率×(各シナリオの収益率－ポートフォリオの期待収益率)2
  1. ポートフォリオの期待収益率を求める（①で求めた6.6がこの値です）
  2. シナリオごとに期待収益率との差（偏差）を求める
  3. 2.で求めた偏差を二乗した値をシナリオごとの生起確率で加重平均する
  4. 3.で求めた数値の平方根を求める
①の【別解】の計算より、シナリオごとの期待収益率はシナリオ1が10.4%、シナリオ2が8.4%、シナリオ3が△5.6%です。それぞれ平均値との差（偏差）は、シナリオ1「10.4%－6.6%＝3.8%」、シナリオ2「8.4%－6.6%＝1.8%」、シナリオ3「△5.6%－6.6%＝△12.2%」となり、各値の二乗を生起確率で加重平均すると、

　3.8%2×0.5＋1.8%2×0.3＋△12.2%2×0.2
＝14.44×0.5＋3.24×0.3＋148.84×0.2
＝7.22＋0.972＋29.768
＝37.96

最後に上記の値（分散）の平方根を求めて標準偏差の値とします。

　37.96＝6.161…％
（小数点以下第3位四捨五入）6.16％

よって、正解は6.16(％)になります。
広告