FP1級過去問題 2021年5月学科試験 問19
問19
以下の表に記載されている固定利付債券の単利計算による最終利回り(空欄①)と割引債券の1年複利計算による最終利回り(空欄②)の組合せとして、次のうち最も適切なものはどれか。なお、税金や手数料等は考慮せず、計算結果は表示単位の小数点以下第3位を四捨五入すること。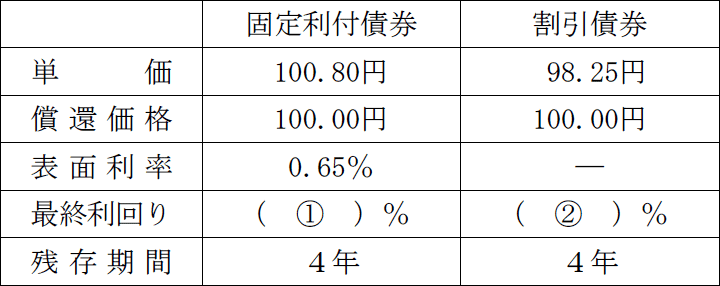

- ① 0.45 ② 0.44
- ① 0.45 ② 0.89
- ① 0.84 ② 0.44
- ① 0.84 ② 0.89
広告
広告
正解 1
問題難易度
肢162.9%
肢220.8%
肢314.4%
肢41.9%
肢220.8%
肢314.4%
肢41.9%
分野
科目:C.金融資産運用細目:4.債券投資
解説
〔①について〕固定利付債券の利回りは次の式で求めます。

0.65+(100-100.80)/4100.80×100
=0.65+(-0.2)100.80×100
=0.45100.80×100=0.4464…%
(小数点以下第3位を四捨五入)0.45%
〔②について〕
割引債とは利子が支払われない代わりに、額面金額から一定額を割り引いた金額が発行価格となるもので、その現在価値は、将来価値(額面100円)に複利現価率を乗じたものとなります。つまり、購入単価、償還価格(100円)、利回り(r)、残存年数の間には次の関係が成り立ちます。
購入単価×(1+r)残存年数=100円
割引債の穴埋め問題では、取得単価を求める問題と最終利回りを求める問題がありますが、どちらも上記の式で対応可能です。本問では残存期間4年の最終利回り(r)を求めたいので、
98.25×(1+r)4=100
(1+r)4=100÷98.25
(1+r)4=1.01781…
(4乗根を求めたいので電卓の√を2回押して)
1+r=1.004423…
r=0.004423=0.4423…%
(小数点以下第3位を四捨五入)0.44%
※割引債券については電卓の2回押しで対応できる4年しか出題されませんが、もし3年とか5年で問われたら、選択肢の利回りで「購入単価×(1+r)残存年数」を計算してどちらが100円に近いかで正解を判別するしかありません。
したがって[1]の組合せが正解です。
広告
広告